○単純梁と両端固定梁の公式
・中心集中荷重
【最大せん断力】
単 純 梁:R=Q=P/2
両端固定梁:R=Q=P/2
【最大曲げモーメント】
単 純 梁:M=PL/4
両端固定梁:M=PL/8
【最大たわみ】
単 純 梁:δ=PL³/48EI
両端固定梁:δ=PL³/192EI.png)
・等分布荷重
【最大せん断力】
単 純 梁:R=Q=pa/2
両端固定梁:R=Q=pa/2
【最大曲げモーメント】
単 純 梁:M=pL²/8
両端固定梁:M=-pL²/12、pL²/24
【最大たわみ】
単 純 梁:δ=5pL⁴/384EI
両端固定梁:δ=pL⁴/384EI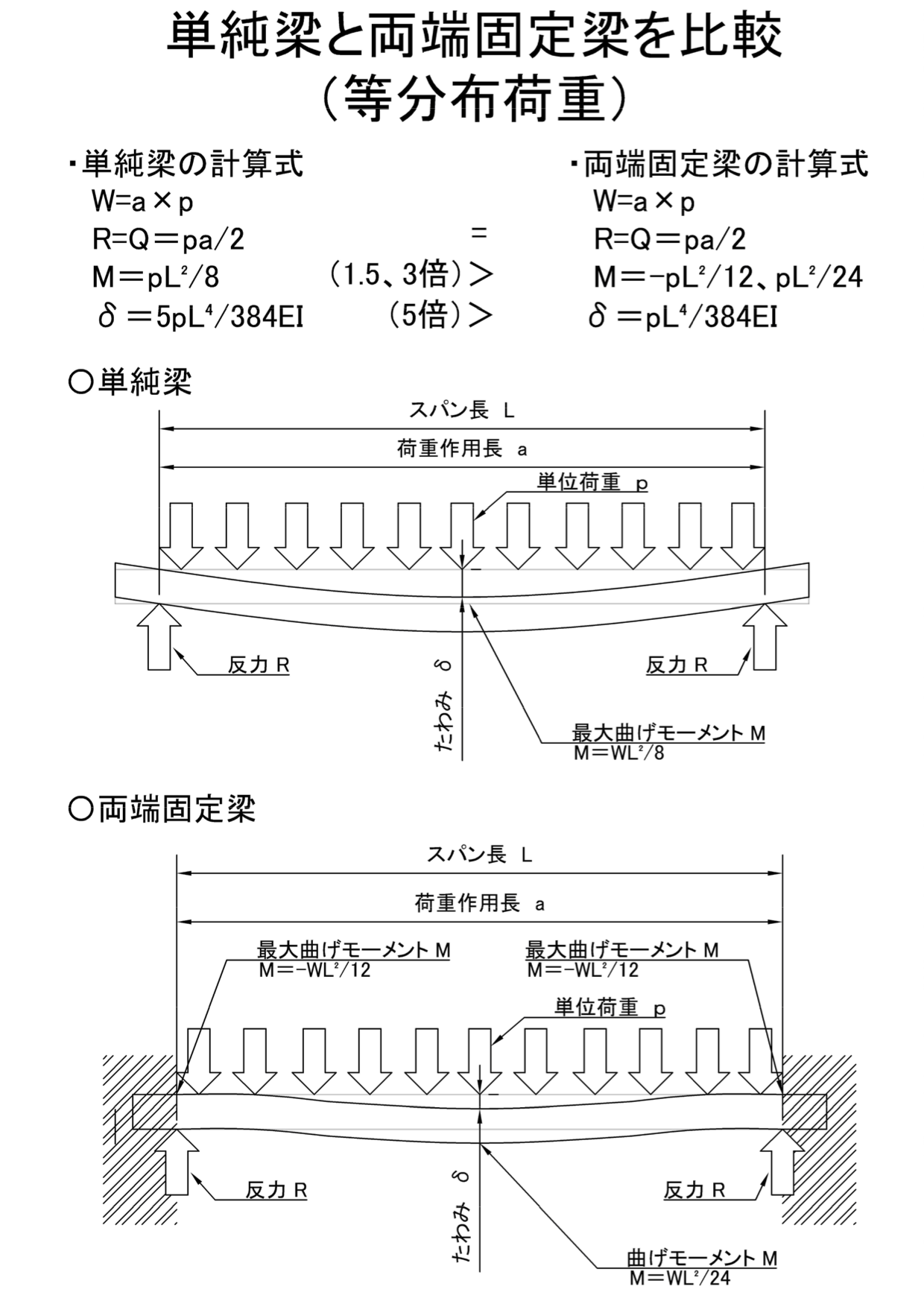
○公式から見る特徴
【最大せん断力】
最大せん断力については集中荷重・等分布荷重どちらも同じである。荷重を負担するのが両端2箇所で同じであるため、同様の値となる。
【最大曲げモーメント】
最大曲げモーメントはどちらの荷重条件でも単純梁のほうが大きくなる。単純梁では支点がモーメントを負担しないため、梁の中央部が最大曲げモーメントとなる。また、発生するモーメントは中央部を頂点とした下に凸の形となるため、正の値のみである。
両端固定梁の最大曲げモーメントは単純梁と比較して単純梁で半分、等分布荷重で2/3である。両端固定梁の場合は梁の中央だけではなく両端部でも曲げモーメントが発生し、両端部が最大曲げモーメントとなる。両端部では負の曲げモーメントが発生し、梁中央部では正の曲げモーメントが発生する。
【最大たわみ】
最大たわみも単純梁のほうが大きくなる。集中荷重では単純梁の最大たわみが両端支持梁と比較して4倍、等分布荷重では5倍である。
○単純梁と両端固定梁の比較
同様のスパン長・荷重条件の場合、単純梁のほうが曲げモーメントやたわみが大きくなるため採用する部材が大きくなる。単純梁のほうが安全だが、両端固定梁の方が経済的である。
注意が必要なのは、両端固定梁の場合は曲げモーメントの向きが変わるので、RC構造の鉄筋の配置のように単一ではない部材の検討の際には注意が必要である。
○単純梁と両端固定梁の使い分け
まず始めに、これら2つの梁はあくまでモデル化された梁であるということを理解するべきである。「完全」な単純梁や両端固定梁はこの世には存在しない。モデルを現実に落とし込む際にどちらのモデルを採用するべきかを設計者が決めなければならない。
例えば、梁の安全を考慮するのであれば梁の中間部の設計には単純梁の最大曲げモーメントを採用し、梁の端部には両端固定梁の最大曲げモーメントを採用することもある。
